Fourier analysis is based on the idea that any time series can be decomposed into a sum of integral of harmonic waves of different frequencies. Hence, theoretically, we can employ a number of harmonic waves to generate any signal.
The Fourier series for an arbitrary function of time f(t)f(t) defined over the interval ((-T/2 < t < T/2 )) is
In the above equation, we can see that the 
In this post, we will use Fourier analysis to filter with the assumption that noise is overlapping the signals in the time domain but are not so overlapping in the frequency domain.
Import libraries, create a signal, and add noise
import pandas as pd
import os, sys
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = [10,6]
plt.rcParams.update({'font.size': 18})
plt.style.use('seaborn')
## Create synthetic signal
dt = 0.001
t = np.arange(0, 1, dt)
signal = np.sin(2*np.pi*50*t) + np.sin(2*np.pi*120*t) # composite signal
signal_clean = signal # copy for later comparison
signal = signal + 2.5 * np.random.randn(len(t))
minsignal, maxsignal = signal.min(), signal.max()
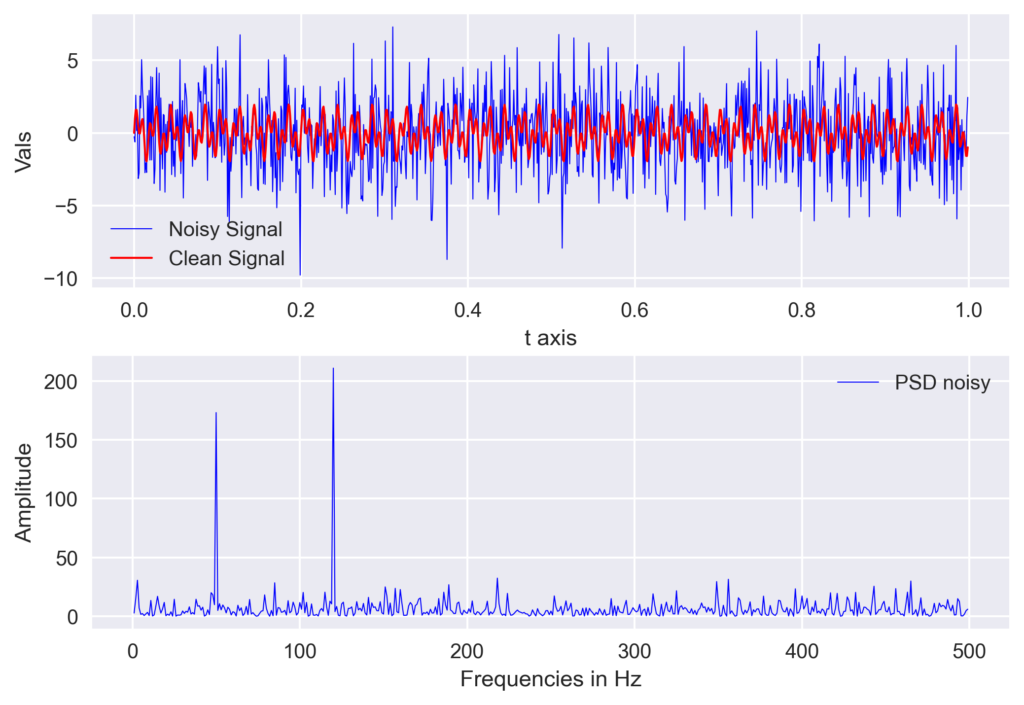
We created our signal by summing two sine functions different frequencies (50Hz and 120Hz). Then we created an array of random noise and stacked that noise onto the signal.
Perform Fast Fourier Transform
## Compute Fourier Transform
n = len(t)
fhat = np.fft.fft(signal, n) # computes the fft
psd = fhat * np.conj(fhat)/n
freq = (1/(dt*n)) * np.arange(n) # frequency array
idxs_half = np.arange(1, np.floor(n/2), dtype=np.int32) # first half index
Numpy’s fft.fft function returns the one-dimensional discrete Fourier Transform with the efficient Fast Fourier Transform (FFT) algorithm. The output of the function is complex and we multiplied it with its conjugate to obtain the power spectrum of the noisy signal. We created the array of frequencies using the sampling interval (dt) and the number of samples (n).
Filter Out the Noise
In the plot above, the two frequencies from our original signal stand out. Now, we can create a filter to remove all frequencies with amplitudes below a threshold.
## Filter out noise
threshold = 100
psd_idxs = psd > threshold # array of 0 and 1
psd_clean = psd * psd_idxs # zero out unnecessary powers
fhat_clean = psd_idxs * fhat # used to retrieve the signal
signal_filtered = np.fft.ifft(fhat_clean) # inverse fourier transform
Visualize the Results
## Visualization
fig, ax = plt.subplots(4,1)
ax[0].plot(t, signal, color='b', lw=0.5, label='Noisy Signal')
ax[0].plot(t, signal_clean, color='r', lw=1, label='Clean Signal')
ax[0].set_ylim([minsignal, maxsignal])
ax[0].set_xlabel('Time (t)')
ax[0].set_ylabel('Values')
ax[0].legend()
ax[1].plot(freq[idxs_half], np.abs(psd[idxs_half]), color='b', lw=0.5, label='PSD Noisy')
ax[1].set_xlabel('Frequency (Hz)')
ax[1].set_ylabel('Amplitude')
ax[1].legend()
ax[2].plot(freq[idxs_half], np.abs(psd_clean[idxs_half]), color='r', lw=1, label='PSD Clean')
ax[2].set_xlabel('Frequency (Hz)')
ax[2].set_ylabel('Amplitude')
ax[2].legend()
ax[3].plot(t, signal_filtered, color='r', lw=1, label='Clean Signal Retrieved')
ax[3].set_ylim([minsignal, maxsignal])
ax[3].set_xlabel('Time (t)')
ax[3].set_ylabel('Values')
ax[3].legend()
plt.subplots_adjust(hspace=0.4)
plt.savefig('signal-analysis.png', bbox_inches='tight', dpi=300)
Real data denoising using power threshold
I have a recording of the accelerometer data using the PhidgetSpatial Precision 0/0/3 High Resolution. I converted that into Miniseed format for easy analysis.
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = [10,6]
plt.rcParams.update({'font.size': 18})
plt.style.use('seaborn')
from obspy import read
from obspy.core import UTCDateTime
otime = UTCDateTime('2021-04-18T22:14:37') # earthquake origin time
filenameZ = 'TW-RCEC7A-BNZ.mseed'
stZ = read(filenameZ)
traces = []
stZ[0].trim(otime, otime+120)
traces.append(stZ[0])
delta = stZ[0].stats.delta
signalZ = traces[0].data/10**6
minsignal, maxsignal = signalZ.min(), signalZ.max()
t = traces[0].times("utcdatetime")
## Fourier Transform
n = len(t)
fhat = np.fft.fft(signalZ, n)
psd = fhat * np.conj(fhat)/n
freq = (1/(delta*n)) * np.arange(n)
idxs_half = np.arange(1, np.floor(n/2), dtype=np.int32)
## Filter out noise
threshold = np.sort(np.abs(psd[idxs_half]))[::-1][300]
psd_idxs = psd > threshold
fhat_clean = psd_idxs * fhat
signal_filtered = np.fft.ifft(fhat_clean)
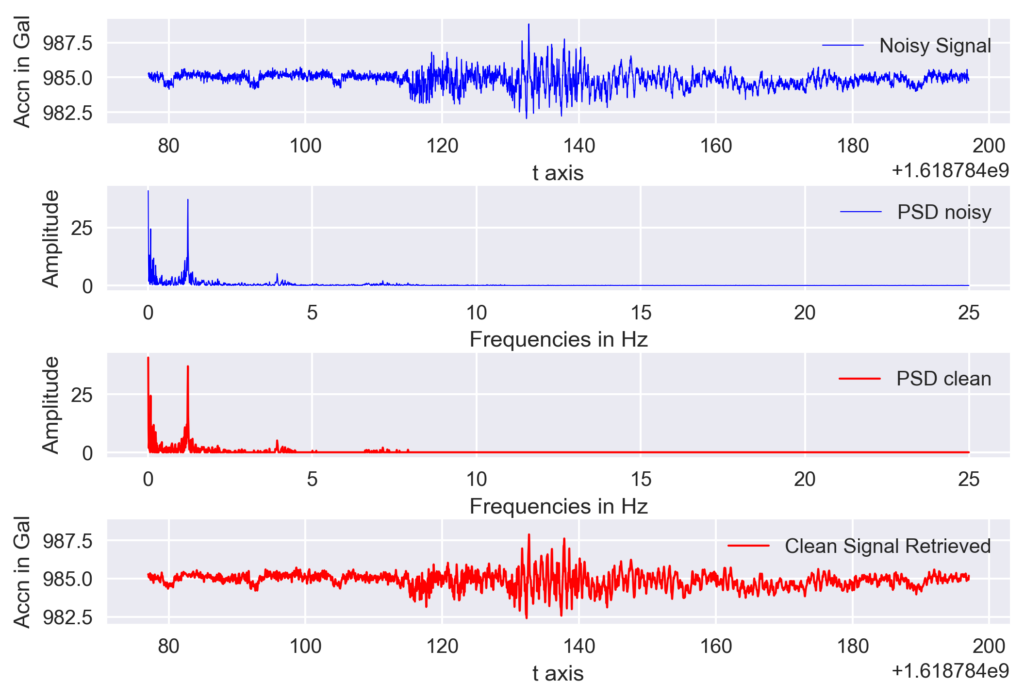
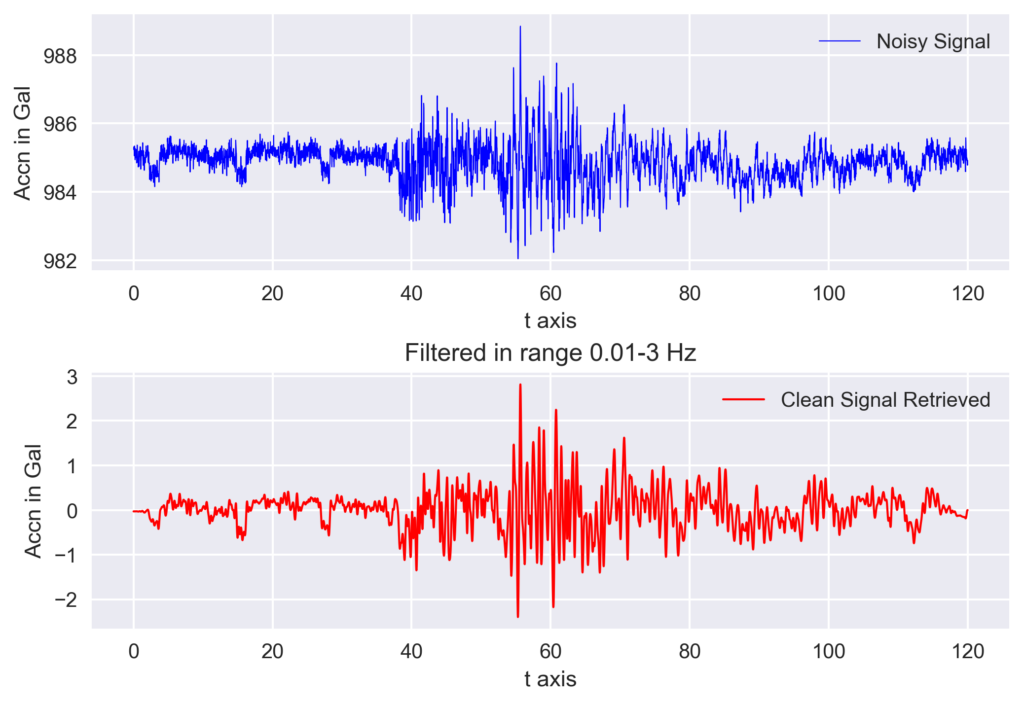
Obspy based filter
Obspy made our task much easier by introducing the filter functions. Here, I made use of the Butterworth-Bandpass filter. For details about different kinds of filters, you can see its documentation.
In this example, I used pass band low corner frequency of 0.01 and high corner frequency of 3 Hz based on the frequency spectrum obtained above.
from obspy import read
from obspy.core import UTCDateTime
otime = UTCDateTime('2021-04-18T22:14:37')
filenameZ = 'TW-RCEC7A-BNZ.mseed'
stZ = read(filenameZ)
stZ[0].trim(otime, otime+120)
signalZ = stZ[0].data/10**6
minsignal, maxsignal = signalZ.min(), signalZ.max()
## Apply bandpass filter
freqmin = 0.01
freqmax = 3
stZ[0].detrend("linear")
stZ[0].taper(max_percentage=0.05, type='hann')
stZ[0].filter("bandpass", freqmin=freqmin, freqmax=freqmax, corners=4, zerophase=True)
signal_filtered = stZ[0].data/10**6
Conclusions
In this post, we only used the basic kind of filter to remove the noise. With the advanced filter, we can have more control in the removal of the frequencies but the overall concept is very similar. In the next post, we will see how we can use wavelets to remove the noise.
References
- Stein, S., & Wysession, M. (2009). An introduction to seismology, earthquakes, and earth structure.
